So, I knew generally, in a mathematically abstract way, how this phenomenon works; but confronting the physical reality often still surprises me. 

In fact, as I thought about it more, I realized that I had encountered the physical system often but without having the time or inclination to do the particular math in detail. So an assignment was born for my students.

Here's the situation. I wanted this rope at the end of the barn to not sag quite so much:

So I tied one little knot:

But I had to look twice at the resulting change in height!

And a modeling question is born — at least for my students: How does the amount of sag in the rope depend on the rope’s length?

Without knot:

With one (small!) knot:

Students can approach this problem in many ways (one hallmark of a good modeling problem), ranging from an empirical study of a rope tied across a doorway and recording sag vs. length, through some curve fitting (three points suffice: the two endpoints and the lowest point in the middle). All the way to an application of the hyperbolic cosine function found at the heart of an ideal catenary. 

Although for most purposes, a parabola is probably close enough.  Hmm… how different are parabolas and catenaries across different scenarios? A nice tangent topic.

A parabola fitted to my rope in GeoGebra:

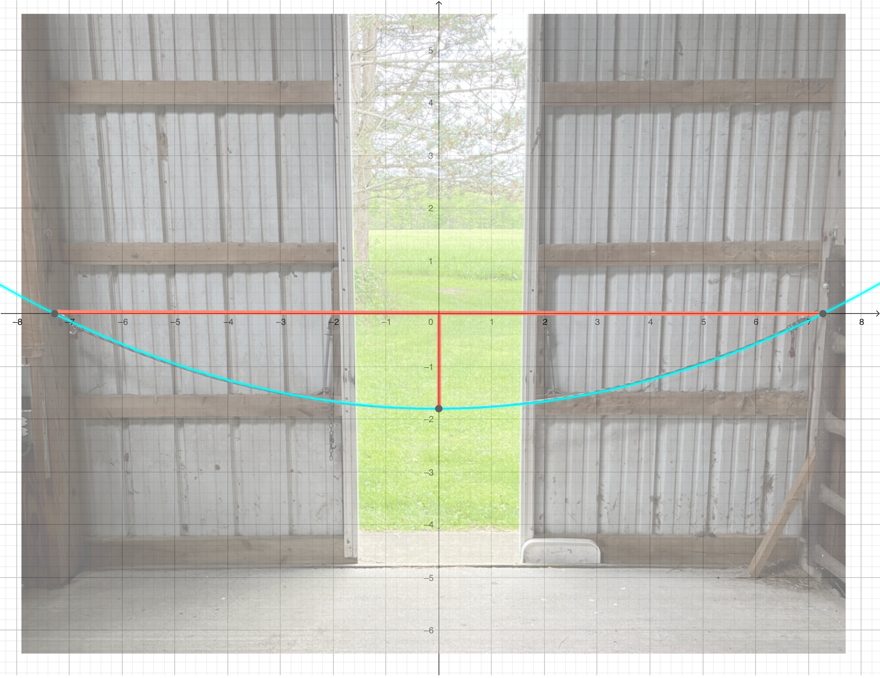
Once a model is in hand, some mathematical computations to get the arc length of a parabola remain. This work can also be approached in a variety of ways, from data collection to simple approximations to some advanced calculus. Encourage students to be creative and use the tools at hand.

At the very least, motivate your students to do some math with all the pictures they’re taking with their phones, and do send us their most interesting work.